História do Calculo
A história do cálculo encaixa-se em vários períodos distintos, de forma notável nas eras antiga, medieval e moderna.
Antiguidade

De acordo com Gauss, Arquimedes, o maior matemático da antigüidade, já apresentava idéias relacionadas ao Cálculo dois séculos antes de Cristo.
Idade Média
Na Idade Média, o matemático indiano Aryabhata usou a noção infinitesimal em 499 d.C. expressando-a em um problema de astronomia na forma de uma equação diferencial básica. Essa equação levou Bhāskara II no século XII a desenvolver uma derivada prematura representado uma mudança infinitesimal, e ele desenvolveu também o que seria uma forma primitiva do "Teorema de Rolle".No século XII, o matemático persa Sharaf al-Din al-Tusi descobriu a derivada de polinômios cúbicos, um resultado importante no cálculo diferencial. No século XIV, Madhava de Sangamagrama, juntamente com outros matemáticos-astrônomos da Escola Kerala de Astronomia e Matemática, descreveu casos especiais da Série de Taylor, que no texto são tratadas como Yuktibhasa.
Idade Moderna

Sir Isaac Newton aplicou o cálculo às suas leis do movimento e a outros conceitos matemáticos-físicos.
Coube a Gottfried Wilhelm von Leibniz e a Isaac Newton recolher essas idéias e juntá-las em um corpo teórico que viria a constituir o cálculo. A ambos é atribuída a simultânea e independente invenção do cálculo. Leibnitz foi originalmente acusado de plagiar os trabalhos não publicados de Isaac Newton; hoje, porém, é considerado o inventor do cálculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o cálculo à física ao passo que Leibniz desenvolveu a notação utilizada até os dias de hoje. O argumento histórico para conferir aos dois a invenção do cálculo é que ambos chegaram de maneiras distintas ao teorema fundamental do cálculo.
Quando Newton e Leibniz publicaram seus resultados, houve uma grande controvérsia de qual matemático (e portanto que país: Inglaterra ou Alemanha) merecia o crédito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou idéias de seus escritos não publicados, que Newton à época compartilhara com alguns poucos membros da Sociedade Real. Esta controvérsia dividiu os matemáticos ingleses dos matemáticos alemães por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integração e Newton com diferenciação. Nos dias de hoje tem-se que Newton e Leibniz descobriram o cálculo independentemente. Leibniz, porém, foi quem deu o nome cálculo à nova disciplina, Newton a chamara de "A ciência dos fluxos".
Desde o tempo de Leibniz e Newton, muitos matemáticos contribuíram para o contínuo desenvolvimento do cálculo.
Idade contemporânea
Na Idade Contemporânea, já no século XIX, o cálculo foi abordado de uma forma muito mais rigorosa por matemáticos como Cauchy, Riemann e Weierstrass. Foi também durante este período que idéias do cálculo foram generalizadas ao espaço euclidiano e ao plano complexo. Lebesgue mais tarde generalizou a noção de integral.Princípios
Limites e Infinitesimais
No século XIX, as infinitesimais foram substituídas pelos limites. Limites descrevem o valor de uma função em um certo ponto em termos dos valores de pontos próximos. Eles capturam o comportamento numérico em baixa escala, como nas infinitesimais, mas utilizando números ordinários. Deste ponto de vista, calculo é uma coleção de técnicas para a manipulação de certos limites. As infinitesimais foram substituídas por números muito pequenos, e o comportamento infinitamente pequeno da função é encontrado pelo limite de números cada vez menores. Limites são fáceis de serem colocados em fundações rigorosas e, por esse motivo, são a abordagem padrão para o cálculo.
Derivadas
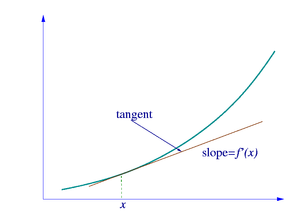
O cálculo diferencial é o estudo da definição, propriedade e aplicações da derivada ou deslocamento de um gráfico. O processo de encontrar a derivada é chamado "diferenciação". Em linguagem técnica, a derivada é um operador linear, o qual forma uma nova função a partir da função original, em que cada ponto da nova função é o deslocamento da função original.
O conceito de derivada é fundamentalmente mais avançado do que os conceitos encontrados em álgebra. Nessa matéria, os estudantes aprendem sobre funções em que o número de entrada gera um número de saída. Por exemplo, se no dobro da função é inserido 3, então a saída é 6, enquanto se a função é quadrática, e é inserido 3, então a saída é 9. Mas na derivada, a entrada é uma função e a saída é outra função. Por exemplo, se na derivada é colocada uma função quadrada, então a saída é o dobro de uma função, porque o dobro da função fornece o deslocamento da função quadrática em qualquer ponto dado da função.
Para entender a derivada, os estudantes precisam aprender a notação matemática. Na notação matemática, um símbolo comum para a derivada da função é um sinal de apóstrofo chamado "linha". Então a derivada de f é f ' (f linha). Isso em notação matemática seria escrito assim:
-
 .
.
Se a função é linear, ou seja, o gráfico da função é uma linha reta, então a função pode ser escrita como y = m x + b, onde:
 .
.
Para determinar o deslocamento da curva, nós usamos os limites:
Integrais
A integral indefinida é a antiderivada, o processo inverso da derivada. F é uma integral indefinida de f quando f é uma derivada de F. (O uso de letras maiúsculas e minúsculas para uma função e sua integral indefinida é comum em cálculo.)
A integral definida insere uma função e extrai um número, o qual fornece a área entre o gráfico da função e o eixo do x. A definição técnica da integral definida é o limite da soma das áreas dos retângulos, chamada Soma de Riemann.
Um exemplo motivacional é a distância (D) viajada em um determinado tempo (t).
Se f(x) no diagrama da esquerda representa a velocidade variando de acordo com o tempo, a distância viajada entre os tempos representados por a e b é a área da região escura s.
Para aproximar a área, um método intuitivo seria dividir em distâncias entre a e b em um número de segmentos iguais, a distância de cada segmento representado pelo símbolo ?x. Para cada segmento menor, nós podemos escolher um valor da função f(x). Chame o valor h. Então a área do retângulo com a base ?x e altura h dá a distância (tempo ?x multiplicado pela velocidade h) viajado naquele segmento. Associado com cada segmento é o valor médio da função sobre ela,f(x)=h. A soma de todos os retângulos dados é uma aproximação da área entre o eixo e a curva, o qual é uma aproximação da distância total viajada. Um valor menor para ?x nos dará mais retângulos e, na maioria dos casos uma melhor aproximação, mas para uma resposta exata nós precisamos fazer o limite em ?x tender a zero.
O símbolo da integração é
 , um S alongado (que significa "soma"). A integral definida é escrita da forma:
, um S alongado (que significa "soma"). A integral definida é escrita da forma:A integral indefinida, ou antiderivada, é escrita da forma:
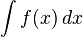 .
.
 .
.
Teorema Fundamental do Cálculo
É afirmado pelo teorema fundamental do cálculo que: Se uma função f é contínua no intervalo [a, b] e se F é uma função cuja derivada é f no intervalo (a, b), então
Considere f uma função contínua de valores reais definida em um intervalo fechado [a, b]. Se F é uma função tal que
 para todo x em [a, b]
para todo x em [a, b]
 .
.
Aplicações

A espiral logarítmica da concha do Nautilus é uma imagem clássica usada para representar o crescimento e a mudança relacionados ao cálculo
A Física faz uso intensivo do cálculo. Todos os conceitos na mecânica clássica são interrelacionados pelo cálculo. A massa de um objeto de densidade conhecida, o momento de inércia dos objetos, assim como a energia total de um objeto dentro de um sistema fechado podem ser encontrados usando o cálculo. Nos sub-campos da eletricidade e magnetismo, o cálculo pode ser usado para encontrar o fluxo total de campos eletromagnéticos. Um exemplo mais histórico do uso do cálculo na física é a segunda lei de Newton que usa a expressão "taxa de variação" que se refere à derivada: A taxa de variação do momento de um corpo é igual à força resultante que age sobre o corpo e na mesma direção. Até a expressão comum da segunda lei de Newton como Força = Massa × Aceleração envolve o cálculo diferencial porque a aceleração pode ser expressada como a derivada da velocidade. A teoria do eletromagnetismo de Maxwell e a teoria da relatividade geral de Einstein também são expressas na linguagem do cálculo diferencial. A química também usa o cálculo para determinar as variações na velocidade das reações e no decaimento radioativo.
O cálculo pode ser usado em conjunto com outras disciplinas matemáticas. Por exemplo, ele pode ser usado com a álgebra linear para encontrar a reta que melhor representa um conjunto de pontos em um domínio.
Na esfera da medicina, o cálculo pode ser usado para encontrar o ângulo ótimo na ramificação dos vasos sanguíneos para maximizar a circulação, e até mesmo determinar o tamanho máximo de moléculas que são capazes de atravessar a membrana plasmática em uma determinada situação, normal ou induzida, em células.
Na geometria analítica, o estudo dos gráficos de funções, o cálculo é usado para encontrar pontos máximos e mínimos, a inclinação, concavidade e pontos de inflexão.
Na economia o cálculo permite a determinação do lucro máximo fornecendo uma fórmula para calcular facilmente tanto o custo marginal quanto a renda marginal.
O cálculo pode ser usado para encontrar soluções aproximadas de equações, em métodos como o método de Newton, iteração de ponto fixo e aproximação linear. Por exemplo, naves espaciais usam uma variação do método de Euler para aproximar trajetórias curvas em ambientes de queda livre.
Fonte: wikipedia



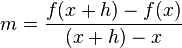
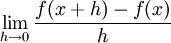

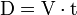

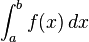
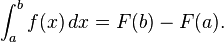
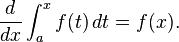

0 Responses to "História do Calculo"
Leave A Comment :